Thuật toán Floyd-Warshall tìm kiếm đường đi ngắn nhất trên đồ thị

Dẫn nhập

Một trong những thuật toán phổ biến nhất và có ứng dụng gần gũi trong đời sống chính là thuật toán tìm kiếm đường đi ngắn nhất trên đồ thị. Trong những bài học tới, hãy cùng nhau đi tìm hiểu về các thuật toán tìm đường đi ngắn nhất trên đồ thị nhé!

Nội dung

Để có thể tiếp thu bài học này một cách tốt nhất, các bạn nên có những kiến thức cơ bản về:

• Các kiến thức cần thiết để theo dõi khóa học
• Đồ thị và cây
• BFS và DFS

Trong bài học ngày hôm nay, chúng ta sẽ cùng nhau tìm hiểu về:

• Các khái niệm quan trọng
• Thuật toán Floyd-Warshall

---

Các khái niệm quan trọng

Trước hết, hãy cùng nhau nhắc lại một số khái niệm.

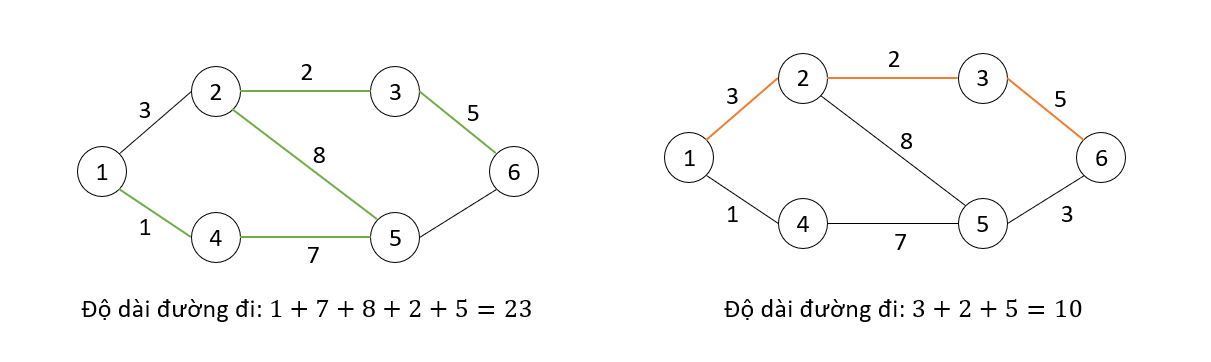
Đường đi giữa hai đỉnh là tập hợp các cạnh liên kết hai đỉnh với nhau.

Độ dài đường đi giữa hai đỉnh là tổng trọng số các cạnh thuộc đường đi giữa hai đỉnh.

Đường đi ngắn nhất giữa hai đỉnh là đường đi giữa hai đỉnh có độ dài nhỏ nhất.

Ví dụ các đường màu xanh và màu cam thể hiện cho đường đi giữa đỉnh 1 và đỉnh 6 trong đó đường màu cam chính là đường đi ngắn nhất và có chiều dài là 10.

---

Thuật toán Floyd-Warshall

Bài toán đặt ra

Cho đồ thị vô hướng gồm n đỉnh và một ma trận trọng số kích thước  trong đó ô  thể hiện một đường đi trực tiếp giữa đỉnh  và đỉnh  có trọng số là giá trị ô . Hãy tính độ dài đường đi ngắn nhất giữa mọi cặp đỉnh trên đồ thị.

Input:

• Dòng 1: Số nguyên dương n thể hiện cho số đỉnh của đồ thị
• Dòng 2…n+1: Mỗi dòng gồm n số nguyên để biểu diễn ma trận trong đó ô  thể hiện một đường đi trực tiếp giữa đỉnh  và đỉnh  có trọng số là giá trị ô .

Output:

• Ma trận kết quả kích thước  trong đó ô  thể hiện độ dài đường đi ngắn nhất giữa đỉnh  và đỉnh 

Ví dụ:

Input	Output
4 2 3 0 1 2 4 6 3 2 3 0 4 4 0 2 5	0 1 0 1 2 0 2 3 2 3 0 3 2 0 2 0

---

Ý tưởng

Ý tưởng của thuật toán Floyd-Warshall (từ đây mình sẽ gọi là Floyd cho ngắn gọn) xuất phát từ nhận xét sau:

Nếu như đường đi ngắn nhất từ đỉnh x đến đỉnh y là  thì đường đi  phải là đường đi ngắn nhất giữa đỉnh  và đỉnh , đường đi   phải là đường đi ngắn nhất giữa đỉnh  và đỉnh .

Thật vậy, giả sử tồn tại đường đi   ngắn hơn đường đi   thì khi đó đường đi ngắn nhất từ đỉnh  đến đỉnh  sẽ là   (trái với giả thiết đường đi ngắn nhất từ đỉnh  đến đỉnh  là ).

Ví dụ: Giả sử ta có đường đi ngắn nhất từ đỉnh 1 đến đỉnh 4 là . Nếu đường đi  lại ngắn hơn đường đi  thì khi đó đường đi ngắn nhất từ đỉnh 1 đến đỉnh 4 phải là  (trái với giả thiết ban đầu). Do đó, không tồn tại bất cứ đường đi nào ngắn hơn.

Do đó, ta có thể phân hoạch việc tính độ dài đường đi ngắn nhất từ đỉnh  đến đỉnh  bằng việc tính độ dài đường đi ngắn nhất từ đỉnh  đến đỉnh  và đỉnh  đến đỉnh . Đây chính là ý tưởng của thuật toán Floyd.

---

Cách cài đặt

Ta có một mảng dist[u][v] với ý nghĩa là độ dài đường đi nhỏ nhất giữa đỉnh u và đỉnh v. Ban đầu, dist[u][v] có giá trị chính là giá trị của ô  trong ma trận cho trước.

Đầu tiên, ta sẽ tiến hành duyệt mọi đỉnh k như là đỉnh trung gian. Tiếp theo, ta sẽ duyệt hai đỉnh u và v với ý nghĩa là ta sẽ chèn thử đỉnh k vào giữa hai đỉnh này. Nếu như dist[u][v] > dist[u][k] + dist[k][v] thì ta sẽ cập nhật lại dist[u][v].

---

Code

#include<bits/stdc++.h>
using namespace std;

const int MaxN = 1 + 1e2;

int n, dist[MaxN][MaxN];

int main(){
    freopen("CTDL.inp","r",stdin);
    freopen("CTDL.out","w",stdout);
    cin >> n;
    for(int i = 1 ; i <= n ; ++i)
    for(int j = 1 ; j <= n ; ++j) cin >> dist[i][j];

    for(int k = 1 ; k <= n ; ++k)
    for(int i = 1 ; i <= n ; ++i)
    for(int j = 1 ; j <= n ; ++j)
    dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);

    for(int i = 1 ; i <= n ; ++i){
        for(int j = 1 ; j <= n ; ++j) cout << dist[i][j] << " ";
        cout << endl;
    }

    return 0;
}

---

Độ phức tạp

Ta thấy thuật toán Floyd sử dụng 3 vòng lặp lồng nhau do đó độ phức tạp ở đây sẽ là .

---

Kết luận

Qua bài này chúng ta đã nắm về Tìm kiếm đường đi ngắn nhất trên đồ thị với thuật toán Floyd.

Bài sau chúng ta sẽ tìm hiểu về Tìm kiếm đường đi ngắn nhất trên đồ thị với thuật toán Dijkstra.

Cảm ơn các bạn đã theo dõi bài viết. Hãy để lại bình luận hoặc góp ý của mình để phát triển bài viết tốt hơn. Đừng quên “Luyện tập – Thử thách – Không ngại khó”.

---

Thảo luận

Nếu bạn có bất kỳ khó khăn hay thắc mắc gì về khóa học, đừng ngần ngại đặt câu hỏi trong phần BÌNH LUẬN bên dưới hoặc trong mục HỎI & ĐÁP trên thư viện Howkteam.com để nhận được sự hỗ trợ từ cộng đồng.