Giới thiệu Linear Regression và hàm hθ(x)

Dẫn nhập

Trong bài trước, chúng ta đã tìm hiểu về MA TRẬN VÀ VECTOR VỚI NUMPY.

Ở bài này Kteam sẽ giới thiệu đến các bạn Linear Regression và hàm h_θ(x).

---

Nội dung

Để theo dõi bài này tốt nhất bạn cần có kiến thức về:

• LẬP TRÌNH PYTHON CƠ BẢN
• Xem qua bài GIỚI THIỆU MACHINE LEARNING VÀ CÀI ĐẶT NUMPY
• Xem qua bài MA TRẬN VÀ VECTOR VỚI NUMPY

Trong bài này chúng ta sẽ cùng tìm hiểu về:

• Các kí hiệu cơ bản trong Machine Learning
• Định nghĩa Linear Regression
• Hàm h_θ(x) trong Linear Regression
• Nhập xuất data từ file với NumPy
• Lập trình hàm h_θ(x) để dự đoán với parameter có sẵn

---

Các kí hiệu cơ bản trong Machine Learning

Đối với Linear Regression, chúng ta sẽ dùng kinh nghiệm (E) là những training set với các cặp giả thiết - kết quả, Kteam đã nhắc đến trong bài GIỚI THIỆU MACHINE LEARNING.

Để làm việc dễ hơn với các thuật toán Machine Learning, chúng ta sẽ quy ước những kí hiệu với training set.

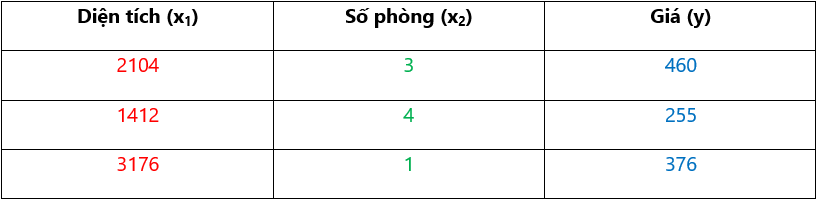
Giả sử ta có training set cho thuật toán dự đoán giá nhà như sau:

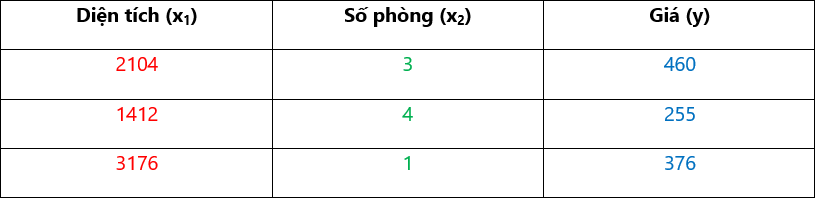
Trong đó:

• m: Số mẫu train (số dòng)
• n: Số feature (input), chính là số cột x.
• x⁽ⁱ⁾: Hàng i của các feature.
• y⁽ⁱ⁾: Hàng i của output.
• x_j⁽ⁱ⁾: Feature j, hàng i.

Lưu ý: Indexing trong Python bắt đầu từ 0.

Ví dụ:

Ở training set trên thì:

• m = 3. n = 2.
• x⁽⁰⁾ = [2104, 3]
• y⁽²⁾ = 376
• x₁⁽²⁾ = 1

---

Linear Regression

Trong thuật toán Regression, chúng ta sẽ tìm 1 hàm số phù hợp với training set.

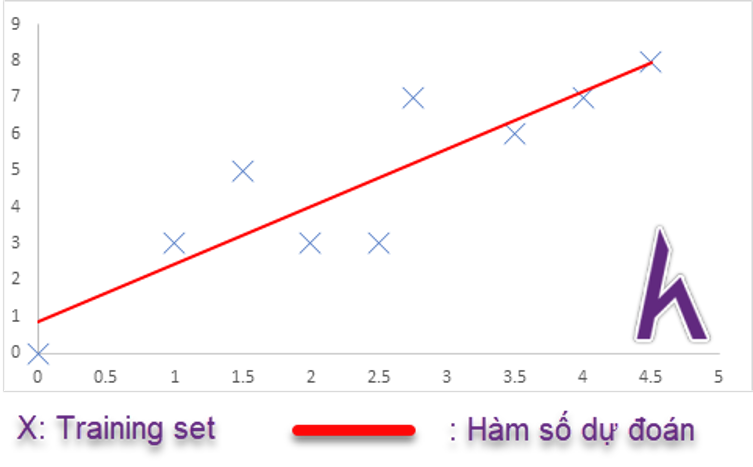
Chúng ta sẽ dựa vào hàm số này để dự đoán output, và vì thuật toán này thuộc nhóm Supervised Learning, chúng ta có thể hoàn toàn nắm được mối quan hệ giữa input và output thông qua hàm số dự đoán: h_θ(x).

---

Hàm h_θ(x)

Hàm h_θ(x) là hàm dùng để dự đoán output trong thuật toán regression. Có thể xem h_θ(x) như một công thức đặc biệt dùng để “tính” ra output. Công thức này còn được gọi là model cho thuật toán Machine Learning của chúng ta.

Công thức của hàm h_θ(x) cho 1 feature (univariate linear regression) là:

y = h_θ(x) = θ₀ + x₁ * θ₁

*Chú thích: Ký hiệu θ đọc là theta.

Và công thức cho nhiều feature (multivariate linear regression) là:

y = h_θ(x) = θ₀ + x₁ * θ₁ +  x₂ * θ_{2 ­} + … +  x_n * θ_n

Trong đó:

• Các x₁, x₂, …, x_n chính là các input của chúng ta.
• Các θ1, θ2, …, θn là các parameter có tác dụng điều chỉnh hàm số cho phù hợp với training set. Ta có thể xem các Theta này là những hệ số quyết định xem input nào ảnh hưởng nhiều đến kết quả, input nào ít ảnh hưởng đến kết quả. Vì đây là hệ số nên trong quá trình debug, hãy nghĩ đây là những con số thực vì biến duy nhất trong hàm này là x, các Theta sẽ được “tính” trong những bài sau
• y chính là kết quả dự đoán của chúng ta.

Ví dụ:

Ta có training set:

 

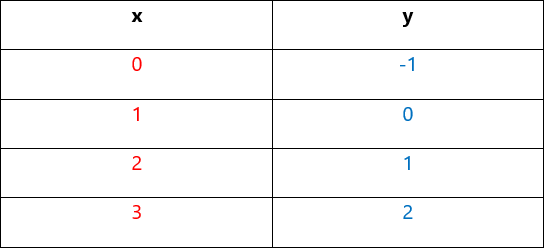
Với parameter θ₀ = -1 và θ₁ = 1 thì hàm h_θ(x) = -1 + x, hoàn toàn khớp với training set:

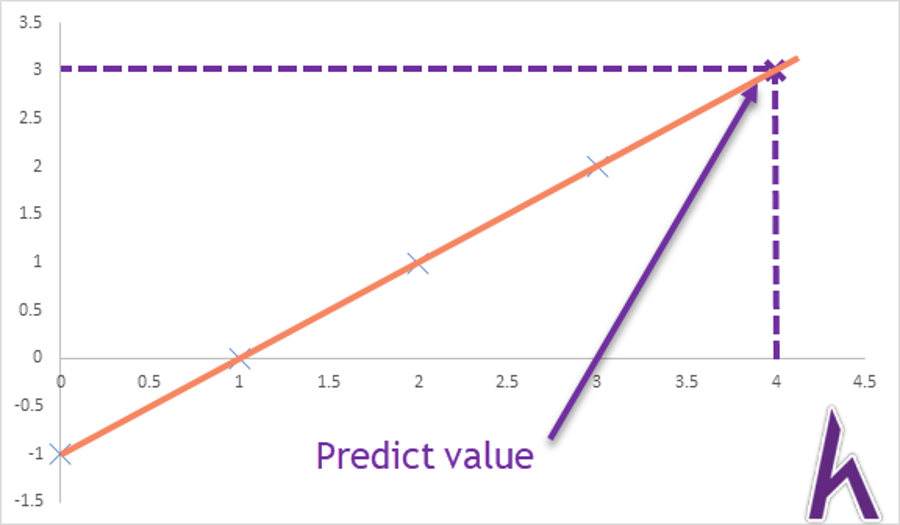
Ta cũng có thể dự đoán nếu x = 4 thì y = h_θ(x) = -1 + 4 = 3.

Vectorize h_θ(x)

Để hàm h_θ(x) có tốc độ xử lí nhanh hơn, chúng ta không thể cứ thực hiện từng phép nhân cho từng feature, sau đó lại cộng lần lượt từng tích lại với nhau. Đây chính là lúc ta áp dụng kiến thức bài trước:PHÉP NHÂN MA TRẬN với khả năng thực hiện nhiều phép nhân cùng lúc và lấy tổng của các tích.

X sẽ là một ma trận gồm các input, ta sẽ có X(i) là một vector ngang (1 * n).

Theta là một vector chứa tất cả các giá trị θ₁, θ₂, …, θ_n.

Ta sẽ có hàm h_θ(x) “vectorized” mới:

y = hθ(x) = X * Theta

Nhưng để thực hiện phép nhân ma trận, ta cần có số cột của X phải bằng số hàng của Theta, với θ₀ ta không có x₀ tương ứng, vì thế ta sẽ thêm x₀ với giá trị luôn bằng 1 ở cột đầu của X.

Ví dụ:

Với training set:

Ta sẽ thêm x₀:

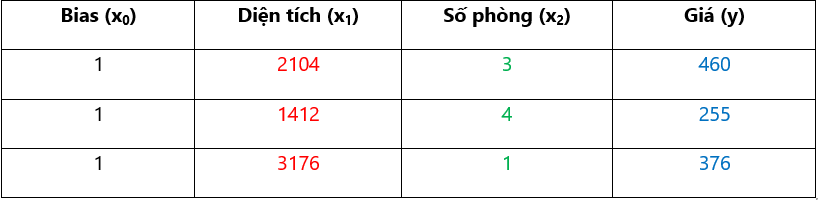
Với bias đồng nghĩa với constant (hằng).

X⁽¹⁾ = [1, 2104, 3]

Theta = [θ₀,

              θ₁,

              θ₂]

Và h_θ(x) = X * Theta = 1* θ₀ + 2104* θ₁ + 3* θ₂. Hoàn toàn giống với hàm h_θ(x) cũ, nhưng với tốc độ nhanh hơn m lần khi thực hiện với toàn bộ training set (ma trận m*n).

Vậy từ giờ, để dự đoán output, ta chỉ cần thực hiện duy nhất 1 phép toán: X * Theta

Mở rộng: các hàm đa thức

Trong thực tế, dữ liệu của chúng ta chẳng bao giờ nằm trên một đường thẳng! Vì thế ta cũng có thể sử dụng những dạng hàm đa thức như hàm bậc 2, bậc 3…

Hàm mũ 2 (square function):

y = h_θ(x) = θ₀ + x * θ₁ + x² * θ₂

Hàm căn bậc 2 (square root function):

y = h_θ(x) = θ₀ + x * θ₁ + x* θ₂

Tuy nhiên, khi sử dụng các hàm có bậc cao hơn, bạn nên cẩn thận vì có thể bạn sẽ gặp vấn đề overfitting (Kteam sẽ giới thiệu trong các bài sau):

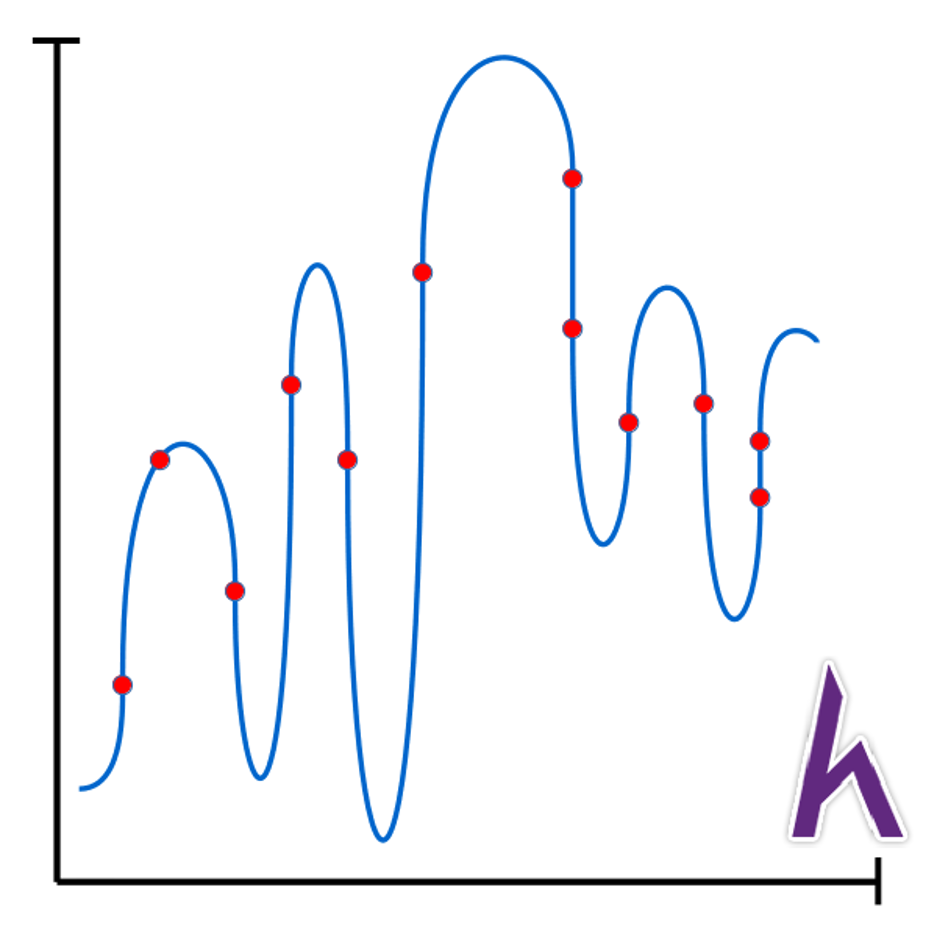
Như bạn thấy, tuy hàm đa thức của chúng ta rất khớp với training set, nhưng thực tế, giá đất không hề bất ổn như thế! Vì vậy, hãy hạn chế dùng các hàm có bậc quá cao hoặc sử dụng các phương pháp chọn bậc cho hàm h_θ(x) Kteam sẽ giới thiệu trong các bài sắp tới.

---

Nhập xuất data với NumPy

Khi làm việc với Machine Learning, chúng ta phải tiếp xúc với lượng data rất lớn, vì thế không thể input data thông qua python prompt được. Ta có thể sử dụng các file dữ liệu để lưu trữ data cho Machine Learning.

Hàm loadtxt với NumPy

Hàm loadtxt dùng để load data từ file *.txt.

np.loadtxt(fname, dtype, delimiter)

Trong đó:

• fname: tên file cần load data (nếu không cùng thư mục gốc với file *.py phải truyền toàn bộ đường dẫn tuyệt đối).
• dtype: kiểu dữ liệu của các element trong file (mặc định là float).
• delimiter: kí tự dùng để phân tách các cột trong file (mặc định là khoảng trắng).

Lưu ý: trừ fname, các parameter khác khi truyền vào phải có key_arg.

Ví dụ:

Bạn có thể download các file text tại:

Bài 3 - Resources

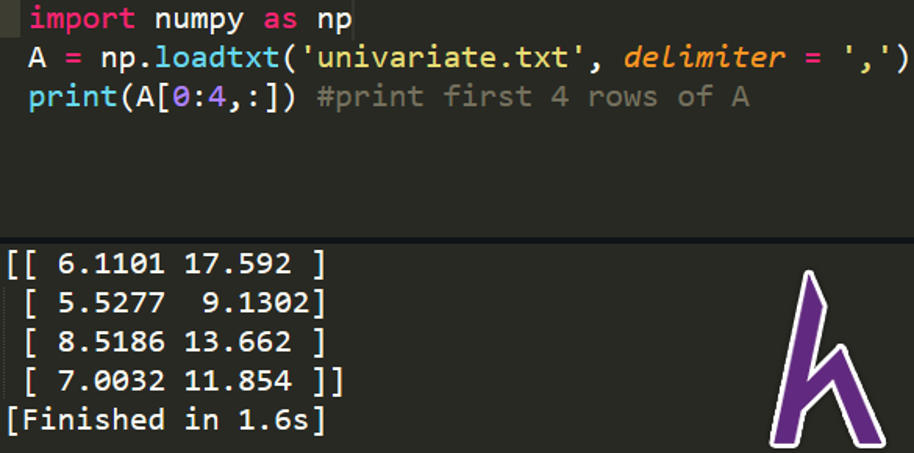
import numpy as np  
A = np.loadtxt(‘univariate.txt’, delimiter = ‘,’) #load univariate.txt to A
print(A[0:4,:]) #print first 4 rows of A

Hàm savetxt với NumPy

Hàm savetxt dùng để lưu ma trận vào file *.txt.

np.savetxt(fname, X, fmt, delimiter)

Trong đó:

• fname: tên file để ghi vào.
• X: ma trận cần ghi vào file.
• fmt: chuỗi định dạng, trong Machine Learning thường dùng để quy định số chữ số thập phân.
• delimiter: kí tự dùng để phân tách các cột.

Ví dụ:

import numpy as np  
A = [ [ 1, 2 ], [ 3, 4 ] ] #create a 2*2 matrix
np.savetxt(‘Saved_A.txt’, A, fmt = ‘%.2f’, delimiter = ‘,’) #save A to Saved_A.txt

File kết quả:

---

Lập trình hàm h_θ(x) để dự đoán output với parameter có sẵn

Univariate problem

Để lập trình được hàm hθ(x) với NumPy, đầu tiên ta load ma trận X và vector Theta. Kteam đã chuẩn bị sẵn cho bạn 2 này trong Resources của bài viết.

Trong vấn đề univariate này chúng ta sẽ dự đoán lợi nhuận của một xe thức ăn từ dân số của thành phố. Cột đầu trong file là dân số, cột thứ hai là lợi nhuận.

import numpy as np  
#import toàn bộ file univariate.txt
X = np.loadtxt(‘univariate.txt’, delimiter = ‘,’)
#import Theta từ file univariate_theta.txt
Theta = np.loadtxt(‘univariate_theta.txt’)

Vì file univariate chứa cả cột y – kết quả dự đoán, chúng ta chưa cần đến cột này để dự đoán kết quả nên ta sẽ bỏ cột này.

Với X, ta cần phải thêm x₀ luôn bằng 1 để thực hiện phép nhân ma trận. x₀ được thêm vào cột đầu tiên của X.

#Lưu cột y
y = np.copy(X[:,-1])
#Chuyển cột đầu (x1) sang cột thứ 2
X[:,1] = X[:,0]
#Đổi cột đầu thành số 1
X[:,0] = 1

Sau khi đã load thành công X và Theta, ta dự đoán bằng cách nhân X với Theta:

#Tính lợi nhuận (đơn vị 10000$)
predict = X @ Theta
#Chuyển lợi nhuận về đơn vị $
predict = 10000 * predict
#in cặp dân số-lợi nhuận đầu tiên (đơn vị dân số: người)
print('%d người : %.2f$' %(X[0,1]*10000,predict[0]))

Ta cũng có thể lưu các kết quả dự đoán vào file mới:

#Lưu kết quả
np.savetxt(‘predicted_value.txt’,predict,fmt = ‘%.6f’)

Bonus: vẽ đường dự đoán so với kết quả thực tế

Để hiểu rõ hàm h_θ(x) hơn, Kteam khuyến khích bạn vẽ hàm bằng thư viện matplotlib.

Đầu tiên, ta sẽ plot các giá trị thực tế:

#Import thư viện
import matplotlib.pyplot as plt
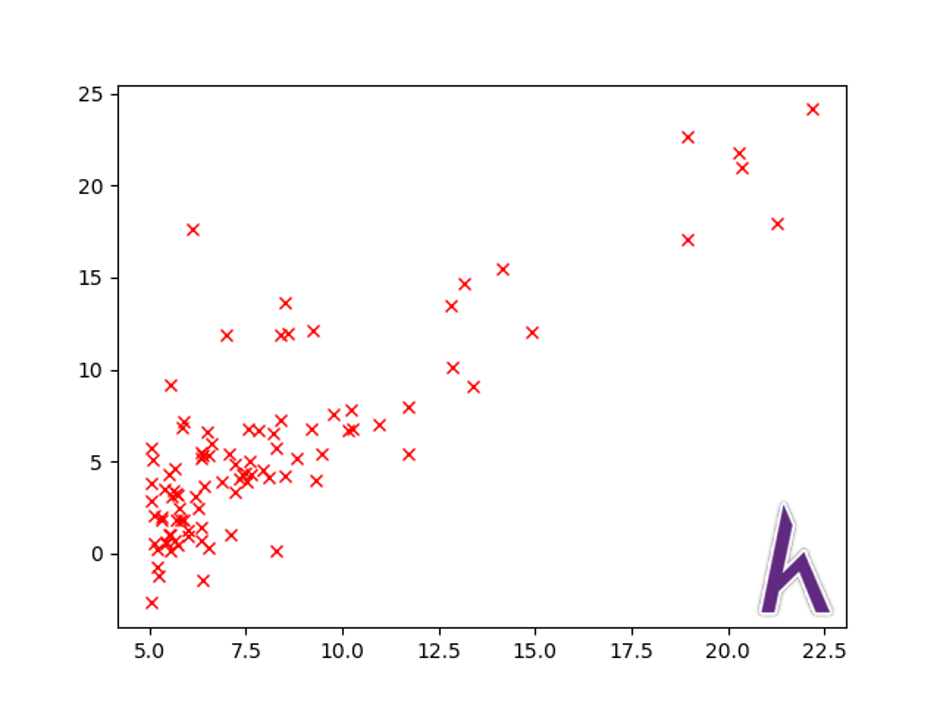
#Plot giá trị thực tế (không lấy cột bias 1 đầu)
#X[:,1:] là x-axis của biểu đồ, không lấy cột đầu; y là y-axis, rx là red x, plot dữ liệu bằng dấu x màu đỏ
plt.plot(X[:,1:],y,’rx’)

Sau đó plot đường dự đoán:

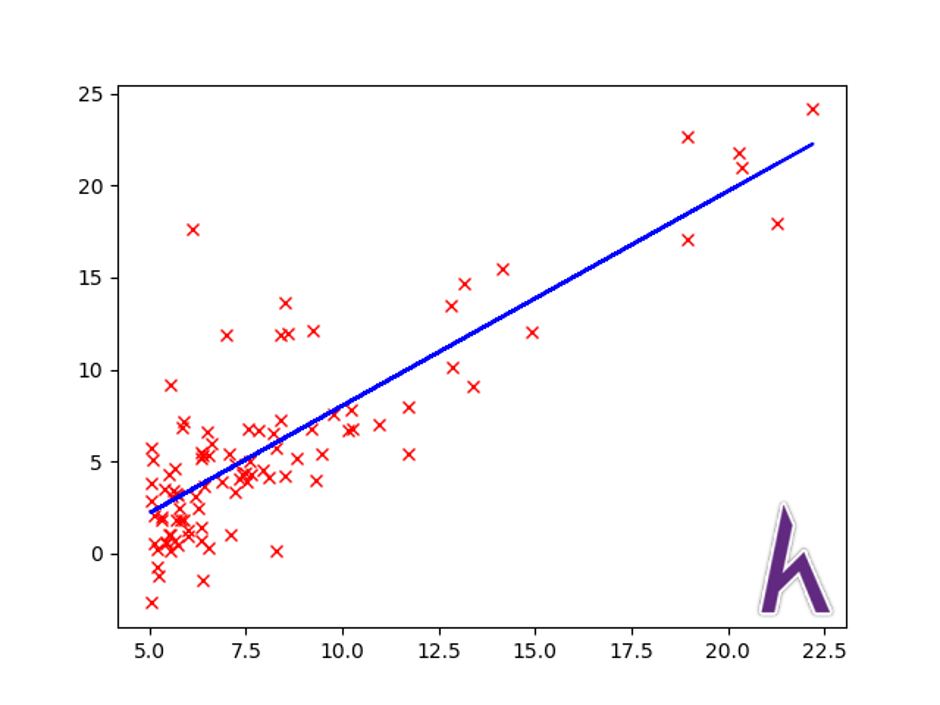
#Plot dự đoán
plt.plot(X[:,1:],predict/10000,’-b’)#ta dùng đơn vị gốc là 10000$, -b là đường thẳng màu xanh
#show kết quả
plt.show()

Toàn bộ source code

import numpy as np
import matplotlib.pyplot as plt
#import toàn bộ file univariate.txt
X = np.loadtxt('univariate.txt', delimiter = ',')
#import Theta từ file univariate_theta.txt
Theta = np.loadtxt('univariate_theta.txt')
#Lưu y
y = np.copy(X[:,-1])
#Chuyển cột đầu (x1) sang cột thứ 2
X[:,1] = X[:,0]
#Đổi cột đầu thành số 1
X[:,0] = 1
#Tính lợi nhuận (đơn vị 10000$)
predict = X @ Theta
#Chuyển lợi nhuận về đơn vị $
predict = 10000 * predict
#in cặp dân số-lợi nhuận đầu tiên (đơn vị dân số: người)
print('%d người : %.2f$' %(X[0,1]*10000,predict[0]))

#Plot giá trị thực tế (không lấy cột bias 1 đầu)
#X[:,1:] là x-axis của biểu đồ, không lấy cột đầu; y là y-axis, rx là red x, plot dữ liệu bằng dấu x màu đỏ
plt.plot(X[:,1:],y,’rx’)
#Plot dự đoán
plt.plot(X[:,1:],predict/10000,’-b’)#ta dùng đơn vị gốc là 10000$, -b là đường thẳng màu xanh
#show kết quả
plt.show()
#Lưu kết quả
np.savetxt('predicted_value.txt',predict,fmt = '%.6f')

Multivariate problem

Ở vấn đề multivariate, chúng ta sẽ dự đoán giá nhà ($) từ kích thước (feet-vuông) và số phong ngủ. Ta sẽ có file multivariate.txt gồm những mẫu thử kích thước-số phòng-giá thực tế. File multivariate_theta.txt sẽ chứa các parameter Theta, giúp ta có thể dự đoán giá.

Đầu tiên, chúng ta sẽ load cả 2 file:

import numpy as np  
#import toàn bộ file multivariate.txt
_X = np.loadtxt('multivariate.txt', delimiter = ',')
#import Theta từ file multivariate_theta.txt
Theta = np.loadtxt('multivariate_theta.txt')

Bước tiếp theo, chúng ta sẽ xóa cột kết quả thực tế và thêm cột x₀ = 1 vào đầu.

#Tạo ma trận X bằng kích thước của _X
X = np.zeros((np.size(_X,0),np.size(_X,1)))
#Thêm cột đầu bằng 1
X[:,0] = 1
#Thêm các cột x1 -> xn
n = np.size(_X,1) - 1
X[:,1:] = _X[:,0:n]

Các bước sau như dự đoán kết quả, in kết quả, lưu kết quả hoàn toàn giống với univariate problem.

#Tính giá nhà (đơn vị $)
predict = X @ Theta
#in bộ diện tích-số phòng-giá đầu tiên
print('%.2f feet-vuông, %d phòng ngủ : %.1f$' %(X[0,1], X[0,2], predict[0]))

#Lưu kết quả
np.savetxt('predicted_value.txt',predict,fmt = '%.2f')

---

Resources

Các bạn có thể download các file text được sử dụng trong bài viết tại:

Bài 3 - Resources

---

Kết luận

Chúc mừng bạn! Qua bài này Kteam đã giúp bạn nắm rõ nguyên lí hoạt động của thuật toán Linear Regression và cách để dự đoán khi đã có sẵn parameter Theta.

Ở bài sau, Kteam sẽ giới thiệu về HÀM J(θ) CHO LINEAR REGRESSION – hàm giúp chúng ta biết được P – độ chính xác của hàm h_θ(x).

Cảm ơn bạn đã theo dõi bài viết. Hãy để lại bình luận hoặc góp ý của mình để phát triển bài viết tốt hơn. Đừng quên “Luyện tập – Thử thách – Không ngại khó”.

---

Thảo luận

Nếu bạn có bất kỳ khó khăn hay thắc mắc gì về khóa học, đừng ngần ngại đặt câu hỏi trong phần BÌNH LUẬN bên dưới hoặc trong mục HỎI & ĐÁP trên thư viện Howkteam.com để nhận được sự hỗ trợ từ cộng đồng.